
TL; DR
LLM을 이용하여 각종 정보를 요약하다보면, 가장 난관에 부딪치는 부분이 수식 파트이다. 특히 논문 정보를 요약하고자 할 때, 수식 파트에 대한 깊이 있는 해석을 얻기 힘들다.
Neuro-symbolic 시스템은 이러한 수식들을 잘 이해하고, 이를 바탕으로 수학적 추론이 가능하게 학습된 모델이다.
본문에 등장하는 Goolgle DeepMind(Alphago로 유명한)의 AlphaGeometry 및 AlphaProof가 여기에 속한다.
본 포스트에서는 Google DeepMind가 AlphaGeometry 및 AlphaProof로 이루어낸 최근 성과를 요약하여 소개해 본다.
* 가독성을 위해 그림 크기를 최소화 했습니다. 클릭 시 확대됩니다.
출처: https://deepmind.google/discover/blog/ai-solves-imo-problems-at-silver-medal-level/
AI achieves silver-medal standard solving International Mathematical Olympiad problems
Breakthrough models AlphaProof and AlphaGeometry 2 solve advanced reasoning problems in mathematics
deepmind.google
AI achieves silver-medal standard solving International Mathematical Olympiad problems
국제 수학 올림피아드 문제 풀이에서 은메달을 획득한 인공지능(AI)
주요 내용
- AlphaProof와 AlphaGeometry 2는 고급 수학적 추론 문제를 해결하는 모델임.
- 인공 일반 지능(AGI)은 과학과 기술의 새로운 영역을 열 가능성을 가지고 있음.
- AI 시스템은 새로운 통찰, 알고리즘, 문제 해결에 도움을 줌.
- 현재의 AI 시스템은 일반 수학 문제 해결에 한계를 가짐.
- AlphaProof는 강화학습 기반의 형식 수학 추론 시스템이고, AlphaGeometry 2는 개선된 기하학 문제 해결 시스템임.
- 이 두 시스템은 올해 국제 수학 올림피아드(IMO)에서 6문제 중 4문제를 해결하여 은메달 수준에 도달함.
복잡한 수학 문제를 해결한 AI의 성능
- IMO는 1959년부터 매년 개최되는 가장 크고 권위 있는 청소년 수학 대회임.
- IMO에서는, 각국의 엘리트 예비 대학 수학자들이 수천 시간 동안 훈련하여 대수학, 조합론, 기하학, 수론에서 매우 어려운 6개의 문제를 해결함.
- IMO는 최근 머신러닝의 대도전이자 AI 시스템의 고급 수학적 추론 능력을 측정하는 기준으로 인정받음.
- Google DeepMind 팀은 AI 시스템을 IMO 문제에 적용하여 솔루션을 제출했으며, 평가는 유명 수학자 팀에 의해 이루어짐.
- AlphaProof는 두 개의 대수학 문제와 하나의 수론 문제를 해결하여 답을 구하고 이를 증명함. 이 중 하나는 대회에서 가장 어려운 문제였음.
- AlphaGeometry 2는 기하학 문제를 증명했으며, 조합론 문제는 해결되지 않음.
- 시스템은 총 42점 만점 중 28점을 획득하여 은메달 수준에 도달함. 금메달 기준은 29점부터 시작하며, 올해 대회에서는 609명 중 58명이 금메달을 획득함.
- 각 문제는 7점 만점이며, 시스템은 해결한 문제마다 만점을 받음.
- 시스템의 IMO 2024 성과는 인간 참가자와 비교하여 은메달 수준을 달성함.

AlphaProof: 추론에 대한 형식적 접근 방식
- AlphaProof는 수학 명제를 형식 언어인 Lean으로 증명하는 시스템임.
- 이 시스템은 사전 훈련된 언어 모델과 AlphaZero 강화 학습 알고리즘을 결합하여 학습함.
- 형식 언어는 수학적 추론을 정확하게 검증할 수 있는 이점을 제공함.
- 자연어 기반 접근법은 많은 데이터를 이용하지만, 중간 추론 단계와 해답이 잘못될 가능성이 있음.
- Gemini 모델을 미세 조정하여 자연어 문제를 형식 명제로 자동 변환하고, 다양한 난이도의 형식 문제 라이브러리를 생성함.
- AlphaProof는 문제에 대해 해결 후보를 생성하고, Lean 언어로 가능한 증명 단계를 검색하여 증명하거나 반증함.
- 검증된 각 증명은 AlphaProof의 언어 모델을 강화하여 더 어려운 문제를 해결할 수 있는 능력을 향상시킴.
- AlphaProof는 수백만 개의 문제를 증명하거나 반증하며, 다양한 난이도와 수학 분야를 포함하여 IMO 준비 기간 동안 학습함.
- 대회 기간 동안에도 자체 생성한 문제 변형의 증명을 강화하여 전체 솔루션을 찾음.
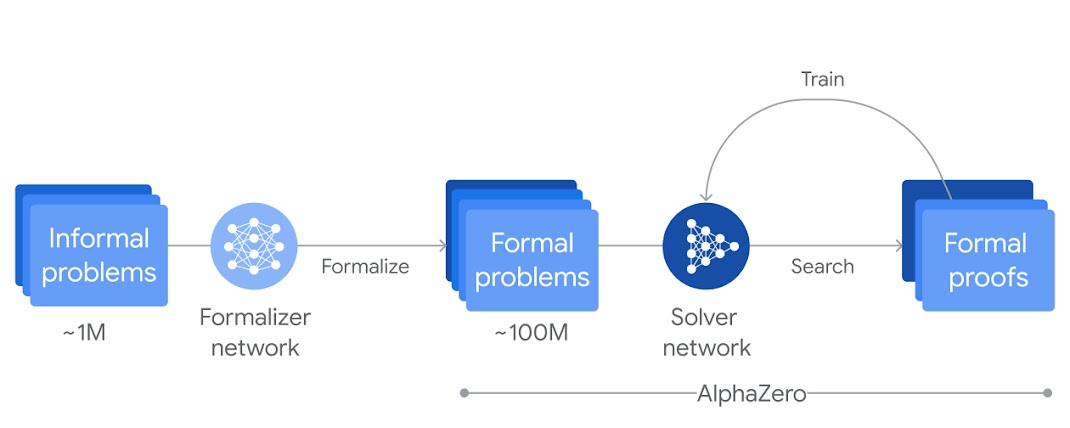
- 훈련 과정:
- 약 백만 개의 비형식 수학 문제를 형식 수학 언어로 번역하는 formalizer 네트워크.
- solver 네트워크는 문제의 증명 또는 반증을 검색하며, AlphaZero 알고리즘을 통해 점진적으로 더 어려운 문제를 해결하도록 훈련됨.
더욱 뛰어난 성능의 AlphaGeometry 2
- AlphaGeometry 2는 AlphaGeometry의 개선된 버전으로, Neuro-symbolic 하이브리드 시스템임.
- Gemini를 기반 언어 모델이 처음부터 훨씬 더 많은 합성 데이터로 사전 학습되어, 더 어려운 기하학 문제를 해결할 수 있게 됨.
- 물체의 이동, 각도, 비율, 거리의 방정식 문제를 포함한 복잡한 기하학 문제를 해결할 수 있음.
- AlphaGeometry 2는 이전 버전보다 두 배 빠른 symbolic 엔진을 사용함.
- 새로운 문제를 받으면 지식 공유 메커니즘을 사용하여 다양한 탐색 트리의 조합을 통해 복잡한 문제를 해결함.
- 이번 대회 전, AlphaGeometry 2는 지난 25년간의 역사적인 IMO 기하학 문제의 83%를 해결했으며, 이는 이전 버전의 53%보다 높음.
- IMO 2024에서 AlphaGeometry 2는 문제 4를 형식화한 후 19초 만에 해결함.
- 문제 4 예시(Link):
- ∠KIL과 ∠XPY의 합이 180°임을 증명하는 문제.
- AlphaGeometry 2는 E를 BI 선 위에 ∠AEB = 90°가 되도록 구성함.
- 점 E는 AB의 중점 L을 활용하여 ABE ~ YBI, ALE ~ IPC와 같은 유사한 삼각형 쌍을 만들어 결론을 증명함.

수학적 추론의 새로운 지평
- IMO 작업의 일환으로 자연어 추론 시스템을 실험함.
- 이 시스템은 Gemini와 최신 연구를 기반으로 하여 고급 문제 해결 능력을 갖추고 있음.
- 형식 언어로 번역할 필요 없이 다른 AI 시스템과 결합 가능함.
- 올해의 IMO 문제에 이 접근 방식을 테스트한 결과, 매우 유망한 결과를 보임.
- 수학적 추론을 발전시키기 위해 다양한 AI 접근 방식을 탐구 중이며, AlphaProof에 대한 기술 세부 사항을 곧 발표할 예정임.
- 미래에는 수학자들이 AI 도구와 협력하여 가설을 탐구하고, 대담한 접근 방식으로 오랜 문제를 해결하며, 증명의 시간 소모적인 요소를 해결하는 시대를 기대함.
- Gemini와 같은 AI 시스템이 수학과 광범위한 추론 능력에서 더 유능해질 것임.
'🟣 AI Study' 카테고리의 다른 글
| LangServe를 이용해 LangChain 앱을 API로 이용하기 (1) | 2024.09.07 |
|---|---|
| Pytorch, 온디바이스 LLM 구동이 가능한 torchchat 소개 (0) | 2024.07.31 |
| Mistral, 새로운 플래그십 모델 Mistral Large 2 출시 (0) | 2024.07.25 |
| 405B 사이즈 모델을 포함한 Llama 3.1 버전 릴리즈 노트 살펴보기 (0) | 2024.07.25 |
| 마구잡이 질문에도 강건한 RAG 시스템 만들기: Query Transformation (0) | 2024.07.20 |





댓글