2023.11.01 - [🔵 AI & ML] - 검색증강생성(RAG) 이해하기 - 01. 벡터 DB 기초
2024.01.27 - [🔵 AI & ML] - 검색증강생성(RAG) 이해하기 - 02. Ragas를 이용한 RAG 파이프라인 평가
TL; DR
RAG 프레임워크에서는, 빠른 벡터 검색을 위해 임베딩한 벡터들을 사전에 군집화 또는 계층화 해놓는다.
이를 통해, 검색 시 모든 벡터를 대조할 필요가 없도록 데이터를 구성하는데 이러한 데이터 구조를 이를 '벡터 인덱스' 라 한다.
벡터 인덱싱 방법으로는 IVF(역파일 인덱스)와 HNSW(계층적 탐색이 가능한 작은 세계) 알고리즘이 가장 잘 알려져 있는데, 여기서는 IVF를 중심으로 설명하면서 벡터 인덱스의 기초가 되는 개념들을 함께 소개한다.
목차
1. 벡터 인덱스와 ANN
2. 역 인덱스와 IVF
3. k-means 클러스터링
4. 코드북과 코드워드
5. 잔차 인코딩
6. 양자화
7. Product 양자화
8. 보로노이 다이어그램
벡터 인덱스와 ANN
RAG 프레임워크를 구축하기 위해 데이터를 벡터로 변환했으면, 이제 벡터를 빠르게 검색할 수 있는 시스템을 구축해야 한다. 기본적인 벡터 유사도 검색 알고리즘인 최근접 이웃, kNN(k-Nearest Neighbor) 기반 검색은 쿼리 벡터와 모든 벡터 간의 거리를 계산하여 가장 가까운 거리에 있는 k개의 벡터를 반환한다. 이 방법은 데이터의 양이 증가할수록 검색 속도가 기하급수적으로 느려지게 된다. 이렇게, 모든 데이터에 대해 유사도 계산이 이루어지는 검색 방식을 완전 검색(exhaustive search) 이라 하기도 한다.
반면, 근사 최근접 이웃, ANN(Approximate Nearest Neighbor) 기반 검색은 정확도를 일부 포기하는 대신 연산 속도를 높이는 것을 목표로 한다. 검색 시 모든 데이터와 유사도를 계산하지는 않기 때문에, 비완전 검색(non-exhaustive search)이라고도 한다. 빠르게 ANN 검색을 수행할 수 있도록, 특정 알고리즘으로 인덱싱된 벡터 데이터 구조를 벡터 인덱스(vector index)라 한다. 벡터 인덱스 알고리즘은 대표적으로 다음과 같은 것들이 있다:
- 그래프 기반 인덱스: HNSW(Hierarchical Navigable Small-World)
- 역 인덱스 기반 인덱스: 역 파일 인덱스(InVerted File index, IVF)
- 해시함수 기반 인덱스(hash-based index): LSH(Locality Sensitive Hashing)
- 트리 기반 인덱스: ANNOY(Approximate Nearest Neighbors Oh Yeah)
이 글에서는 먼저, IVF에 대해 알아본다.
역 인덱스와 IVF
역 인덱스(inverted index, 또는 역색인)는 키워드를 통해 데이터를 찾아내는 방식이다. 보통 책의 가장 뒷부분에서 볼 수 있는, '찾아보기' 파트가 역 인덱스의 예로 볼 수 있다. 역 인덱스 방식에서는 데이터가 증가하더라도 검색해야 할 행의 수(키워드)가 증가하는 것이 아니라, 역 인덱스가 가리키는 ID의 배열 값(페이지 번호)만 추가되기 때문에 큰 속도 저하 없이 빠른 검색이 가능하다.

그럼 벡터 검색 시스템에서 어떻게 역 인덱스를 적용할 수 있을까? 미리 벡터 간 유사도를 계산하여 구성된 클러스터(cluster, 군집) 및 그 중심점(centroid)을 구하고, 각 클러스터에 벡터 ID를 할당하는 방식으로 역 인덱스 시스템을 구상할 수 있을 것이다. 그럼, 검색 시스템은 쿼리에 대해 각 클러스터의 중심점들과 대조를 수행하여, 쿼리가 속하는 클러스터를 찾으면 되기 때문에 효율적인 검색이 가능해진다. 이렇게 벡터 검색 시스템에 역 인덱스 방식을 적용한 것을 역 파일 인덱스, IVF(InVerted File index)라 한다. 그럼, IVF 벡터 인덱싱 과정을 이해하는 데에 필요한 개념들을 알아보자.
k-means 클러스터링
IVF의 핵심은 데이터를 사전에 유사한 것들끼리 모아 몇 개의 군집으로 묶어놓는 것이다. 즉, 클러스터링 작업이라 할 수 있는데 k-means(k-평균) 클러스터링은 IVF에서 가장 보편적으로 사용되는 클러스터링 알고리즘이다. k-means 클러스터링은, 별도의 레이블이 없는 데이터에 적용할 수 있는 비지도(unsupervised) 클러스터링 알고리즘 중 하나이다.
k-means 클러스터링의 과정은 다음과 같다:
- 먼저 k개 만큼의 클러스터에 대한 중심점(centroid)을 임의로 설정한다.
- 중심점과 다른 데이터에 대한 거리 계산을 반복하면서, 중심점이 해당 군집을 더 잘 표현할 수 있도록(=평균에 가깝도록) 중심점 좌표를 업데이트한다.
- 이 작업을 중심점의 변화가 미비해지는 어떤 기준에 이를 때까지 충분히 반복한다.
- 최종적으로, 데이터들은 가장 가까운 중심점에 해당하는 클러스터로 할당되면서 k개의 클러스터가 형성된다.
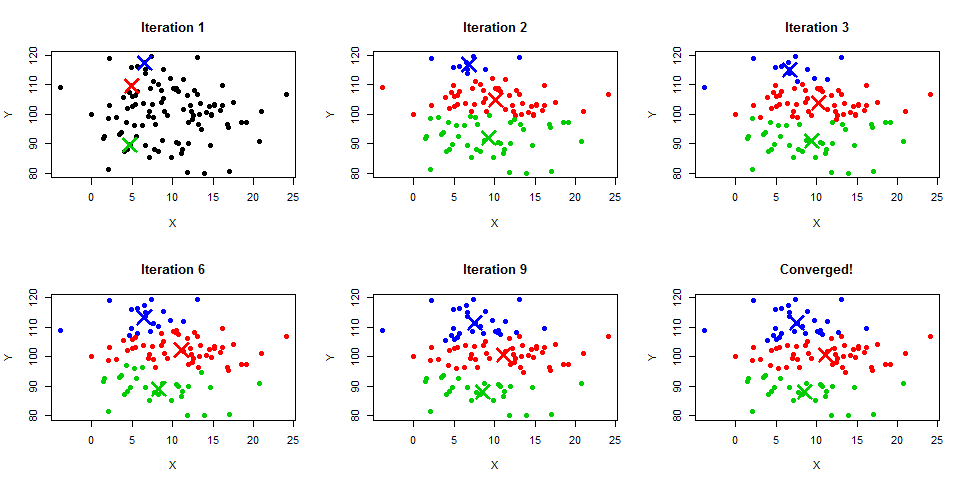
k-means 클러스터링이 어떻게 IVF에서 벡터 검색을 빠르게 할 수 있는지 생각해보자. 만약 100개의 데이터를 10개의 클러스터로 나누었다면, 쿼리가 입력되었을 때 100개 데이터에 모두 유사도 계산을 수행하지 않고 10개 클러스터의 대푯값(k-means 클러스터링에서는 중심점)들에 대해서만 유사도 계산을 수행한다. 이후, 입력 쿼리가 속하는 클러스터의 데이터에 대해서만 세부 검색을 다시 수행할 수도 있다. 만약 데이터가 균일하게 10개씩 클러스터링되었다면, 20회 이하의 계산으로 검색을 마칠 수 있다.
물론, 대푯값이 해당 클러스터를 100% 대표할 수 없기에 완벽한 정확도의 검색은 어렵지만, 이렇게 벡터 공간을 사전에 세분화해놓으면 데이터 양이 많아질 때 검색 효율을 크게 높일 수 있다.
코드북과 코드워드
k-means 클러스터링을 수행했으면, 이제 그 결과를 저장해놓아야 한다. 각 벡터 데이터에 클러스터의 번호 및 대푯값을 할당하는 과정에서 사용되는 개념이 코드북(codebook)과 코드워드(codeword)이다. k-means 클러스터링을 수행하면 각 클러스터의 중심점이 계산되는데, 이러한 중심점의 집합을 코드북이라 할 수 있다. 그리고, 해당 중심점의 클러스터에 속하는 벡터 데이터들이 코드워드이다. 쿼리가 입력되면, 쿼리는 모든 데이터가 아닌 코드북에 있는 중심점들에 대해 유사도 계산을 먼저 수행하고, 그 후 쿼리가 속하는 코드북에 속한 코드워드 데이터들과 유사도 계산이 이루어지게 된다.
코드북과 코드워드는 클러스터링 결과를 벡터 인덱스에 적용하는 과정에서 관습적으로 사용되는 용어일 뿐이므로, 참고만 하면 되겠다.
- 코드북: k-means 클러스터링으로 계산된 중심점들의 집합
- 코드워드: 중심점에 해당하는 각 클러스터에 속한 데이터들
잔차 인코딩
잔차 인코딩(residual encoding)은 위에서 설명한 코드워드에 해당하는 데이터를 표현할 때 적용되는 메모리 효율화 방법 중 하나이다. 잔차(residual)라는 단어는 통계나 모델 학습 시 오차를 계산하는 과정에서 종종 보았을 텐데, 여기서의 잔차 인코딩은 '코드워드 데이터들을 코드북(중심점)과의 차이로 나타내어 저장하는 방법'을 말한다.
이렇게 데이터를 표현하면 데이터의 범위가 훨씬 줄어들고, 그럼으로써 더 적은 수의 숫자로 데이터를 표현할 수 있다. 그리고, 원본 데이터의 좌표를 얻으려면 잔차에 다시 중심점 데이터를 더하는 역연산만 해주면 된다.
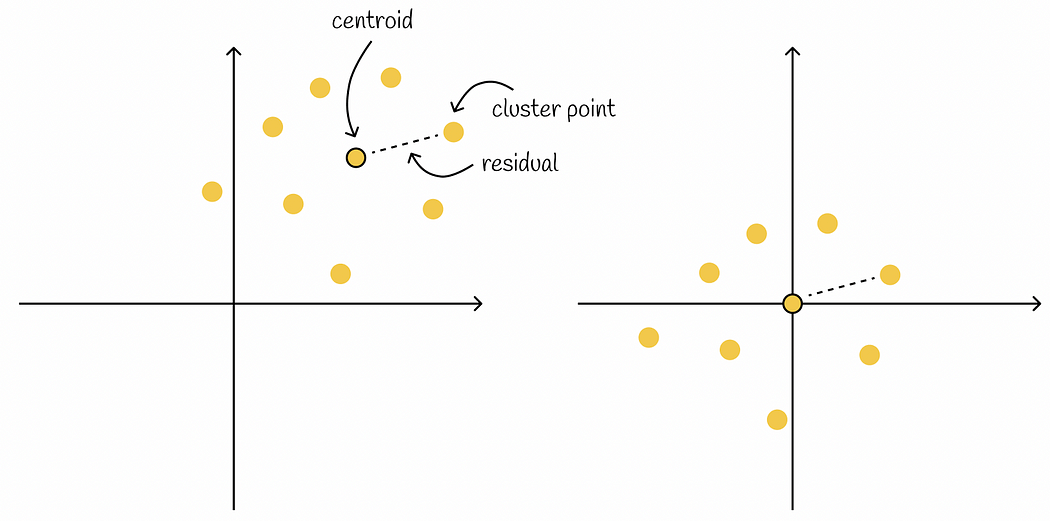
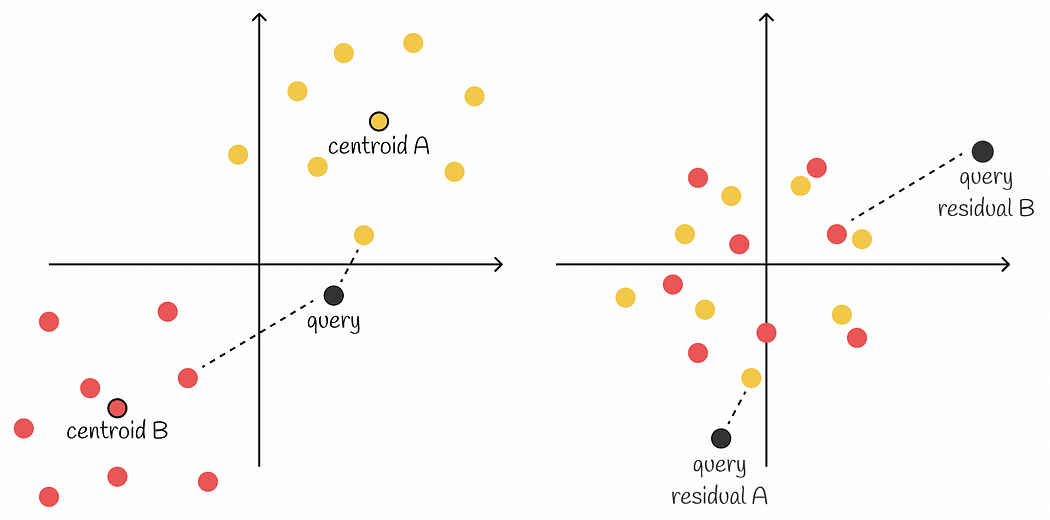
잔차 인코딩을 적용하면, 더 적은 수의 숫자로 데이터를 표현할 수 있다는 개념을 한 번 더 짚고 넘어가보자. 동일한 벡터 공간에서, 서로 다른 클러스터의 데이터들은 같은 좌표값을 가질 수 없다. 하지만, 중심점과의 거리는 같을 수 있으므로 잔차는 같은 값을 가질 수 있다. 잔차의 값이 같더라도, 해당 벡터가 다른 클러스터에 속한다는 정보가 있으므로 두 데이터를 구분할 수 있다.
그럼, k-means 클러스터링을 수행하고, 중심점 및 클러스터링 데이터를 코드북과 코드워드 형태로 저장하고, 잔차 인코딩을 적용하는 과정을 간단한 형태로 한 번 구현해보자. 이는 이해를 돕기 위한 예제로, 실제 벡터 검색 시스템의 구현 양상과는 다를 수 있다.
from sklearn.cluster import KMeans
import numpy as np
# 임의 데이터 생성
np.random.seed(25)
data_points = np.random.rand(12, 2)
# k-means 클러스터링
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(data_points)
이 예제에선 2차원으로 구성된 12개의 간단한 데이터셋을 이용하였고, k-means 클러스터링으로 3개의 클러스터를 생성하였다. 클러스터링 결과를 다음과 같이 시각화할 수 있다.
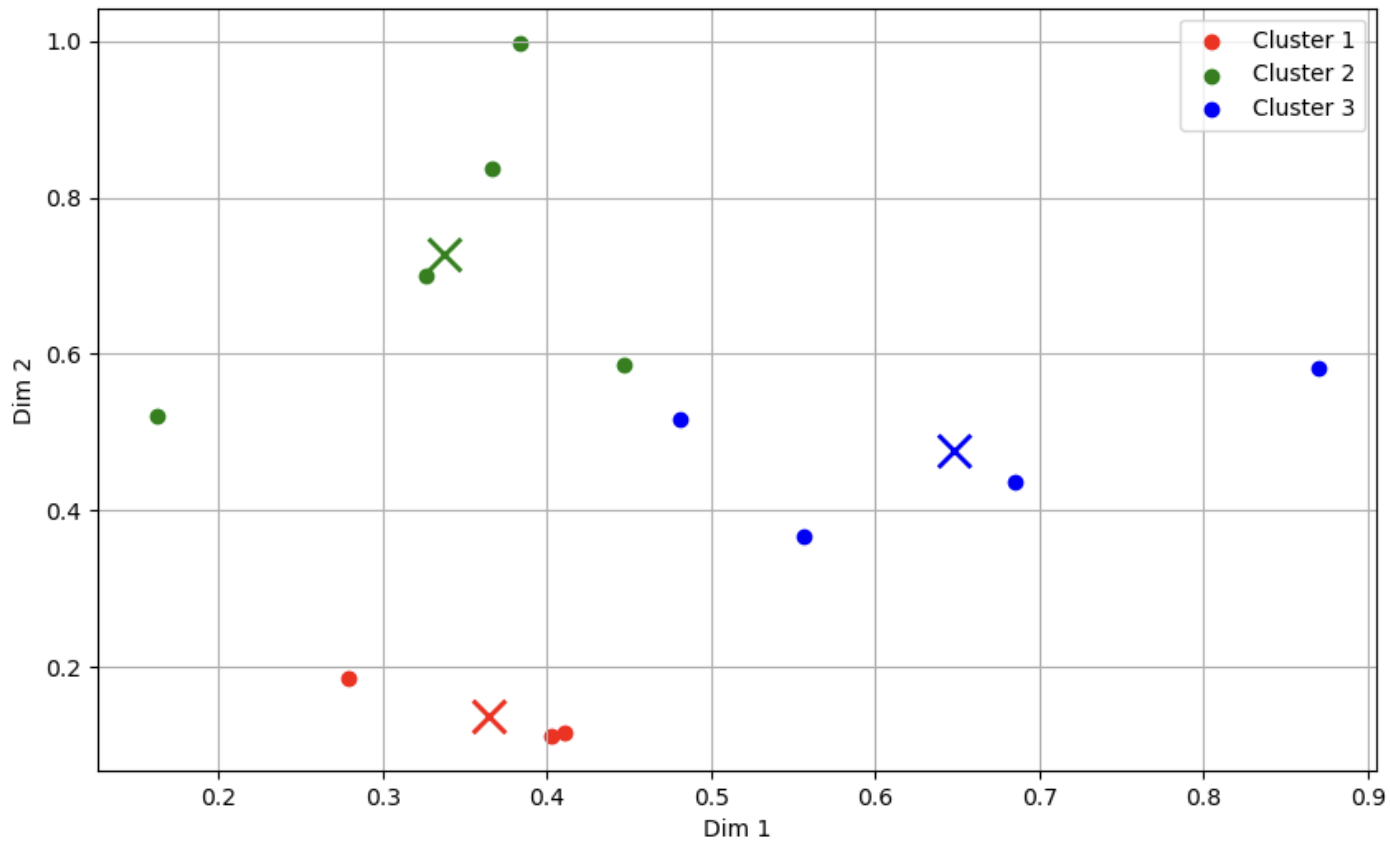
이제 k-means 클러스터링 결과를 코드북, 코드워드의 저장한다. 코드워드를 저장할 때는, 잔차 인코딩을 적용해 보도록 하자. 아래와 같이 코드를 구성하면, 저장된 벡터 인덱스 결과를 확인할 수 있다.
# 코드북(중심점) 및 클러스터 인덱스 저장
codebook = kmeans.cluster_centers_
# 잔차 인코딩 후 클러스터 인덱스와 함께 코드워드 데이터 저장
codewords = [data_points[i] - codebook[cluster_indices[i]] for i in range(len(data_points))]
cluster_indices = kmeans.predict(data_points)
codewords_with_indices = [(cluster_indices[i], codewords[i]) for i in range(len(data_points))]
# 벡터 인덱스 결과 저장
ivf_index = {
"codebook": codebook,
"codewords": codewords_with_indices
}
ivf_index
출력된 결과는 다음과 같다. 코드북은 3개 군집에 대한 중심점의 좌표, 코드워드는 클러스터의 번호 및 각 벡터의 중심점에 대한 잔차값이다.
{'codebook': array([[0.3641016 , 0.13877583],
[0.33690195, 0.72785311],
[0.64816629, 0.47586765]]),
'codewords': [(2, array([0.22195785, 0.10640928])),
(0, array([-0.08526266, 0.04713541])),
(0, array([ 0.04699853, -0.02140028])),
(2, array([ 0.03680246, -0.03825659])),
(2, array([-0.09193696, -0.10878733])),
(0, array([ 0.03826413, -0.02573513])),
(1, array([ 0.1101289 , -0.14240799])),
(1, array([-0.17491685, -0.20713432])),
(1, array([-0.01085082, -0.02866687])),
(1, array([0.0294926, 0.1085214])),
(2, array([-0.16682334, 0.04063465])),
(1, array([0.04614618, 0.26968779]))]}
이제 입력 쿼리가 들어오면, 쿼리는 코드북의 중심점에 대해 계산이 이루어지고 해당 쿼리가 속한 클러스터에 해당하는 코드워드에서 다시 유사도를 계산하여 세부 검색을 수행할 수도 있다.
클러스터 내의 벡터들과 중심점 간 거리를 미리 계산한 거리 행렬(distance matrix)를 함께 저장해놓는 경우도 있다. 하지만 이는 인덱싱 시간과 필요 저장 공간을 증가시킬 것이므로 상황에 따라 선택하여 수행해야 할 것이다.
양자화
복잡하게 느껴질 용어 설명 전에 미리 말하자면, 우리가 위에서 수행한 과정이 일련의 양자화 과정이다. 양자라는 단어의 의미는 다양하지만 벡터 인덱스 과정에서의 양자화는 검색 및 데이터 저장 효율을 높이기 위해 데이터 표현을 더 간단한 형태로 변환하는 과정을 말한다.
양자화는 보통 부동 소수점(floating point) 형식으로 표현되는, 연속적인 벡터 공간을 클러스터링 등을 통해 이산적인 부분 공간으로 나누어 표현한다. 이는 정수(integer) 등 다양한 표현이 있을 수 있는데, 기존 데이터 표현보다 검색이나 메모리 사용 측면에서 더 효율적인 방식이어야 한다. 이 글에서는 자세한 설명을 줄이겠지만, 여기에는 부동 소수점의 표현보다 정수 형태의 데이터 표현이 데이터 검색 및 저장 측면에서 효율적이라는 배경 지식이 깔려 있다.
양자화를 엄밀한 표현으로 적으면 다소 어렵게 느껴지지만, 벡터 인덱스에서의 양자화는 다음과 같이 정리할 수 있다:
- 유사 벡터들을 묶어 클러스터를 구성하고, 해당 벡터들을 클러스터에 해당하는 번호나 대푯값(중심점)으로 표현한다.
- 소수점 형태(연속)로 표현된 벡터를 정수 등의 더 간단하고 검색 효율적인 형태(이산)로 표현한다.
Product 양자화
우리가 앞서 수행한, 전체 데이터에 클러스터링을 수행하고 그 결과로 데이터를 표현한 것도 일종의 양자화이다(이를 coarse quantization, 즉 성긴 양자화라고도 한다). 하지만, 보통 벡터 인덱스에서 양자화라고 하면 이 단계 다음에 수행되는 추가적인 양자화 과정인 product 양자화(product quantization, PQ)*를 지칭하는 경우가 일반적이다.
Product 양자화는 벡터 데이터를 더 작은 벡터들로 나눈 서브벡터(subvector) 공간에 각각 양자화를 추가로 수행하는 것을 말한다. Product 양자화에서는 위에서 설명한 k-means 클러스터링과 코드북 및 코드워드, 잔차 인코딩 개념이 그대로 사용될 수 있다. 우리가 원 벡터를 복수의 서브벡터로 나누었으므로, 벡터는 서브벡터 수만큼의 중심점 번호로 표현될 것이다. 이렇게 변환된 벡터 표현을 PQ 코드라 한다. 먼저 설명한 코드북, 코드워드와 유사한 표현으로 생각하자. 참고로, product 양자화가 적용된 IVF 벡터 인덱스를 IVF-PQ라 표현하고 적용되지 않은 것을 IVF-Flat이라 표현한다.
* '곱 양자화'로 번역할 수 있지만, 해당 번역이 직관적이지 않아 원 용어를 그대로 서술한다. 벡터 공간을 분할하고, 이렇게 생성된 하위 공간을 조합하여(이를 product라 표현) 원래 벡터 공간을 근사한다는 의미의 용어이다.
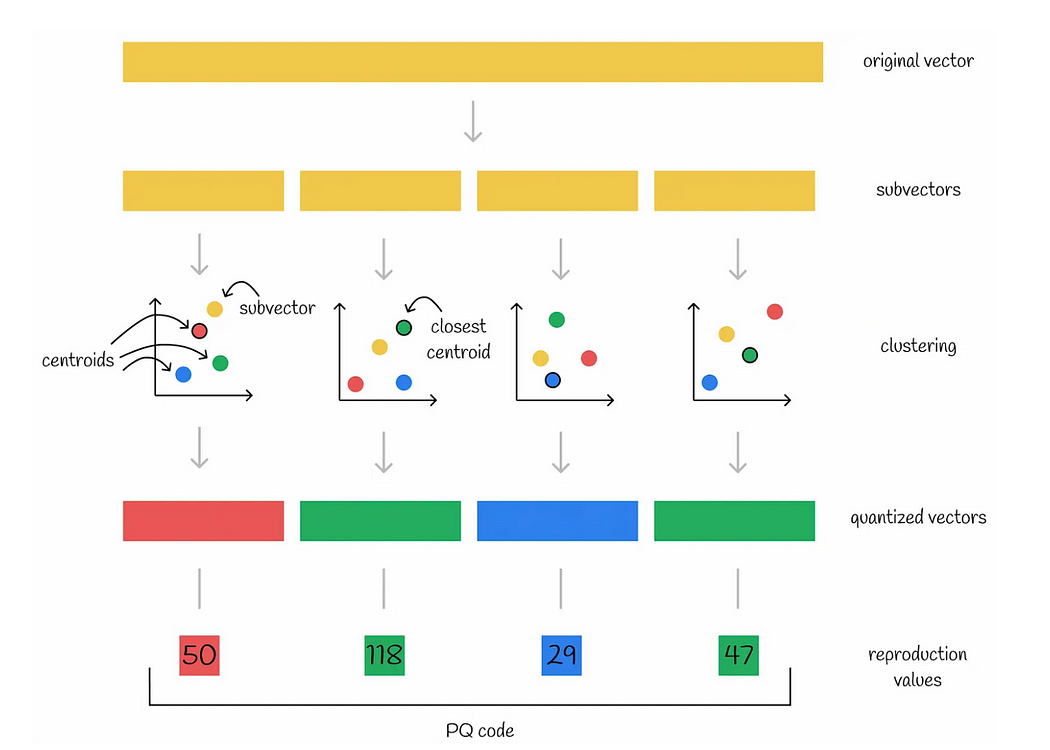
위 그림에서, 만약 128차원의 벡터를 32차원의 서브벡터 4개로 나눈다고 해 보자. 각 서브벡터에서 클러스터링(k-means와 같은)을수행하고, 잘려진 벡터 조각들은 각각 하나의 클러스터에 할당될 것이다. 이 클러스터 정보를 정수로 표현한다면, 최종적으로 벡터는 128개의 부동 소수점 대신 4개의 정수로 표현될 것이다. 이렇게 벡터를 양자화하여 나온 정수 배열이 PQ 코드이다. 검색을 수행할 때는, 입력 쿼리도 PQ 코드로 변환되어 검색이 이루어지게 된다.
보로노이 다이어그램
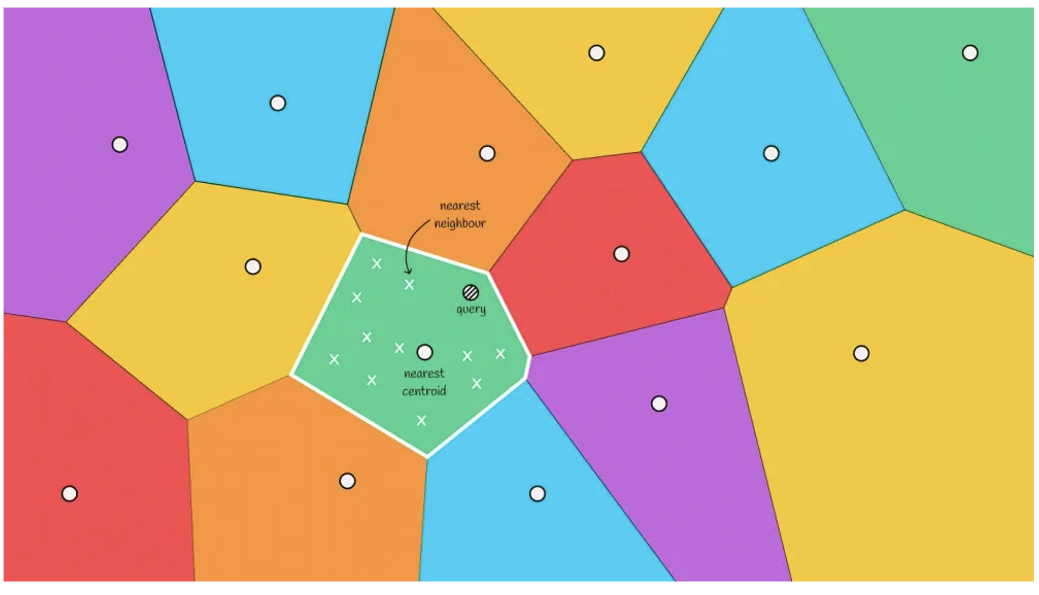
보로노이 다이어그램 (Voronoi diagram)은 벡터 공간 분할에 대한 개념을 설명할 때 종종 등장하는 개념이므로 의미를 알아두면 좋다. 보로노이 다이어그램은 러시아의 수학자 조지 보로노이(Georgy F. Voronoy)의 이름을 따서 지어졌다. 이 다이어그램은 수학적인 원리를 바탕으로 평면을 여러 영역으로 분할하는 그림으로 표현되는데, 이 과정에서 주어진 데이터 세트 내의 각 데이터와 가장 가까운 데이터들을 계산하여 경계를 나눈다. 이렇게 하면, 각 데이터는 자신과 가까운 데이터들로 구성된 보로노이 셀(Voronoi cell)이라는 영역을 갖게 된다. 이 영역은 리전(region)이나 파티션(partition)으로도 불리며, 각 보로노이 셀 내부에는 셀 형성 기준이 되는 중심점(centroid)이 존재한다. 보로노이 다이어그램에서 두 데이터 사이의 경계를 결정할 때는, 수직 이등분선을 이용한다.
예를 들면, k-means로 계산한 중심점을 기준으로 보로노이 다이어그램을 만들어 벡터 공간을 분할할 수도 있다. 클러스터링과 보로노이 다이어그램은 유사한 것 같지만, 클러스터링은 데이터 포인트(점)에 초점을 맞춘 개념이라면 보로노이 다이어그램은 데이터가 속한 공간에 초점을 맞춘 개념이기 때문에 그 활용 양상이 다를 수 있다.
마치며
이 포스트에서는 IVF의 기본 원리 및 벡터 인덱스와 관련된 몇 가지 기초 개념에 대해 알아보았다. 내용을 요약하면 다음과 같다.
1. 벡터 인덱스는 검색을 빠르게 할 수 있도록 벡터들을 미리 군집화하거나 계층화하여 전처리하는 데이터 구조이다.
2. IVF는 역 인덱스의 원리를 사용하는데, 정해진 특정 수의 클러스터를 인덱스로 사용한다.
3. 벡터 인덱싱을 위해 k-means 클러스터링이 이용될 수 있고, 클러스터링 결과를 코드북과 코드워드 형태로 저장한다.
4. 양자화는 연속적인 벡터 데이터 표현을 이산적인 데이터 표현으로 변환하여 효율을 높인다.
5. Product 양자화는 벡터를 서브벡터로 분할하여, 각 서브벡터 공간에 양자화를 수행한다. 결과적으로, 벡터는 PQ 코드로 표현된다.
6. 보로노이 다이어그램은 벡터 공간을 분할하는 알고리즘 중 하나로, k-means 클러스터링과 함께 벡터 인덱싱 과정에 종종 이용된다.
다음 포스트에서는 IVF보다도 더 널리 이용되는 HNSW 벡터 인덱스나, 코사인 유사도 등의 벡터 유사도 검색 메트릭(metric)에 대해서도 다루어 볼 예정이다.
참고자료
'🟣 AI Study' 카테고리의 다른 글
| 검색증강생성(RAG) - 그래프 기반 벡터 인덱스 HNSW(Hierarchical Navigable Small World) (0) | 2024.02.25 |
|---|---|
| OpenAI의 동영상 생성 모델 'Sora' Technical Report 읽어보기 (0) | 2024.02.17 |
| 검색증강생성(RAG) - Ragas를 이용한 RAG 파이프라인 평가 (0) | 2024.01.27 |
| LLM 이해하기 - LLM의 기초 개념 (3) | 2024.01.14 |
| Microsoft, 2.7B의 경량 규모 언어 모델 출시: Phi-2 (2) | 2024.01.10 |





댓글