TL;DR
이전 포스트에서는 역 인덱스 기반의 IVF 벡터 인덱스를 소개했다.
IVF와 함께 벡터 데이터베이스에서 가장 많이 사용되고 있는 벡터 인덱스 알고리즘으로,
벡터 데이터를 계층형 그래프로 구성하여 표현하는 HNSW(Hierachical Navigable Small World)이 있다.
이 포스트에서는 HNSW를 이해하는 데에 필요한 개념들을 소개하면서, HNSW의 원리를 이해해보도록 한다.
* HNSW 논문 링크(Malkov & Yashunin., 2016): https://arxiv.org/abs/1603.09320
목차
1. Small World
2. NSW(Navigable Small World)
3. Skip List
4. HNSW(Hierachical Navigable Small World)
5. HNSW의 사용
Small World
Small world(작은 세계)는 1960년대 심리학자 스탠리 밀그램(Stanley Milgram)의 실험에 기반하고, 1998년 던컨 와츠(Duncan Watts)와 스티븐 스트로가츠(Steven Strogatz)가 발표한 논문 'Collective dynamics of small-world networks'을 통해 널리 알려진 네트워크 이론이다. Small world는 인간 관계에서 몇 단계만 거치면 서로 연결되어 있다는 것을 보인 이론이다. Small world는 해당 이론을 바탕으로 한 '케빈 베이컨 게임'으로도 잘 알려져 있다. 헐리우드에서 상당한 다작 배우인 케빈 베이컨(Kevin Bacon)은, 같이 출연한 영화로 몇 단계(보통 6단계 이내)만 건너면 대부분의 배우와 연결된다고 하여 만들어진 게임이다.

Small world의 이론적인 특징은, 평균 경로 거리가 작고 군집 계수(clustering coefficient)가 높다는 것이다. 평균 경로 거리가 작다는 것은, 네트워크에서 임의의 두 사람을 골라도 적은 단계로 연결될 수 있다는 것을 의미한다. 그리고, 군집 계수가 높다는 것은 어떤 사람의 친구들이 그 친구들 서로도 아는 사이일 가능성이 높다는 것을 의미한다.
NSW(Navigable Small World)
kNN(k-Nearest Neighbors) 알고리즘 기반으로도 벡터 인덱스를 구성하여 검색할 수 있지만, 고차원 데이터를 다룰 때에나 업데이트가 잦은 실시간성 데이터에서 kNN 기반 검색 시스템은 비효율성을 가진다. 새로운 데이터가 추가될 때마다 모든 데이터에 대해 유사도를 다시 계산해야하기 때문이다. 이를 조금 어렵게 표현하면, kNN 기반 검색은 고차원 데이터에 대한 차원의 저주(cusre of dimentionality)를 보이며 동적(dynamic) 데이터에는 적절하지 않다고 할 수 있다. 이를 개선하기 위해, 근사 이웃만을 탐색하여 검색 속도를 높이는 다양한 k-ANN(k-Approximate Nearest Neighbors) 알고리즘들이 제안되었다.
NSW(Navigable Small World) 알고리즘은 상기한 문제점을 보완하기 위해, small world의 개념을 이용한다. NSW에서는 인덱싱 및 검색 과정에서 임의로 선택된 진입 노드(entry point)에서 시작하여 지정한 수준까지만 탐색을 수행한다. Small world 이론에 의하면, 이렇게 적은 단계의 탐색만 거쳐도 충분히 쿼리와 근사한 노드를 반환할 수 있기 때문이다. 이렇게 검색 양을 제한하기 때문에, 데이터의 양이 많아져도 kNN 기반 검색 시스템에 비해 빠른 인덱싱 및 검색이 가능하다.
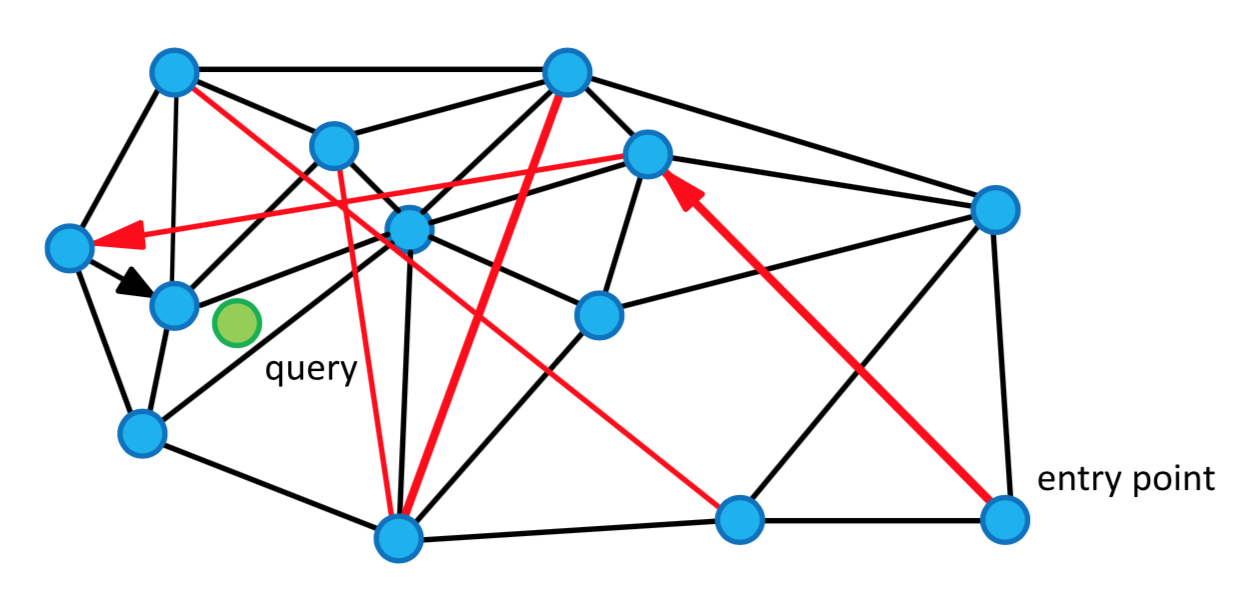
Skip List
Skip list는 linked list 자료 구조를 더 효율적인 검색이 가능하도록 계층적으로(hierarchical) 확장하여 구성한 검색 알고리즘이다. Skip list의 가장 하위 레벨의 층은 모든 데이터 노드를 포함하며, 상위 레벨의 층으로 갈수록 더 적은 수의 노드를 가진 linked list로 구성된다. 검색에 사용되는 링크는 다음 노드로 이어지는 기본 링크와 다른 레벨의 노드로 이어지는 링크로 구성된다. 이러한 링크 구조는 전체 구조를 가로지르며 데이터를 빠르게 탐색할 수 있는 경로를 형성한다.
Skip list는 이러한 검색 구조를 통해, linked list에 비해 로그 시간 안에 수렴하는($O(logn)$), 빠른 검색 속도를 제공한다. 또한, skip list에 새로운 데이터를 추가할 때 무작위로 레벨을 할당받기 때문에 균형잡힌 구조를 유지하면서도 검색 성능을 보장한다. Skip list가 linked list를 계층화한 구조인 것처럼, HNSW는 NSW에 계층화를 적용한 구조이다.
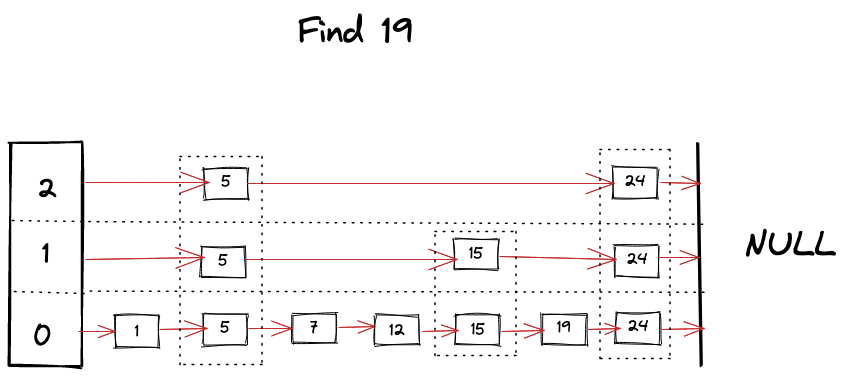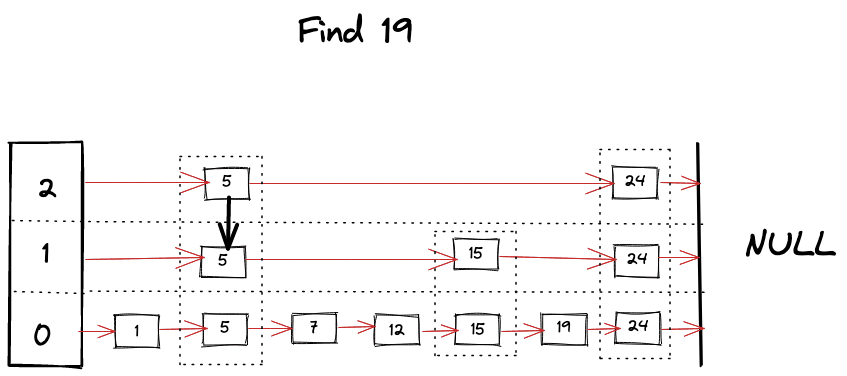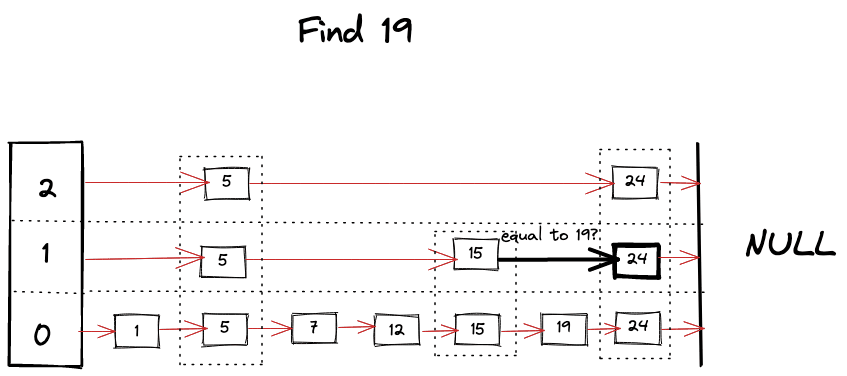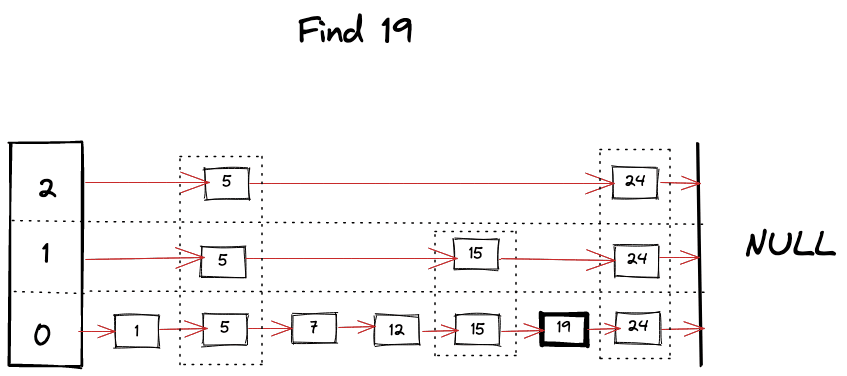
HNSW(Hierachical Navigable Small World)
HNSW(Hierachical Navigable Small World)는 NSW에 skip list의 개념을 적용하여, NSW 그래프를 계층화한다. 가장 아래의 레이어는 모든 노드를 포함하며, 위로 갈수록 더 적은 노드로 구성된 형태의 그래프로 구성된다. 일반적인 HNSW의 벡터 인덱싱 및 탐색의 주요 양상은 다음과 같이 정리할 수 있다.
- HNSW는 먼저, 최상위 레벨의 레이어에 있는 진입점(entry point)에서 탐색(또는 인덱스 구축)을 시작한다. 이 레벨은 전체 데이터셋을 대표하는 노드이다.
- 만약 새로 추가된 노드가 기존 진입점보다 더 높은 레벨을 가지면, 해당 노드로 진입점이 업데이트될 수 있다.
- 새 노드가 추가될 때, 그 노드의 레벨은 확률적으로 결정된다. 노드가 더 상위 레벨을 가질 확률은 지수적으로 감소하게 설정되어 있으므로, 상위 레벨의 레이어로 갈수록 더 적은 수의 노드를 갖게 된다.
- 각 레벨에서, 노드는 그 레벨의 가까운 이웃(nearset neighbors)을 계산해 서로 연결되며 그래프를 형성하는데 각 노드의 이웃 수는 미리 정의된 파라미터($M$)에 의해 제한된다. 각 노드는 자신의 레벨과 같거나 낮은 레벨의 이웃들과만 연결된다.
- 노드를 추가할 때, 진입점부터 시작하여 해당 노드의 레벨 이하의 모든 레벨에서 가장 가까운 이웃을 설정한 수($M$)만큼 찾아 그래프에 할당한다.
- 쿼리가 입력되면, HNSW는 탐욕(greedy) 알고리즘을 사용하여 각 단계에서 최적의 이웃을 선택한다. 이 과정은 하위 레벨로 이동하며 반복 수행되며, 각 노드는 자신의 레벨과 같거나 낮은 레벨의 이웃들로만 이동한다.
- 설정한 탐색 종료 기준에 따라 탐색을 종료하고, 최종 검색 결과를 반환한다.
HNSW 벡터 인덱싱 및 검색을 간략히 나타내면 다음 그림과 같다.
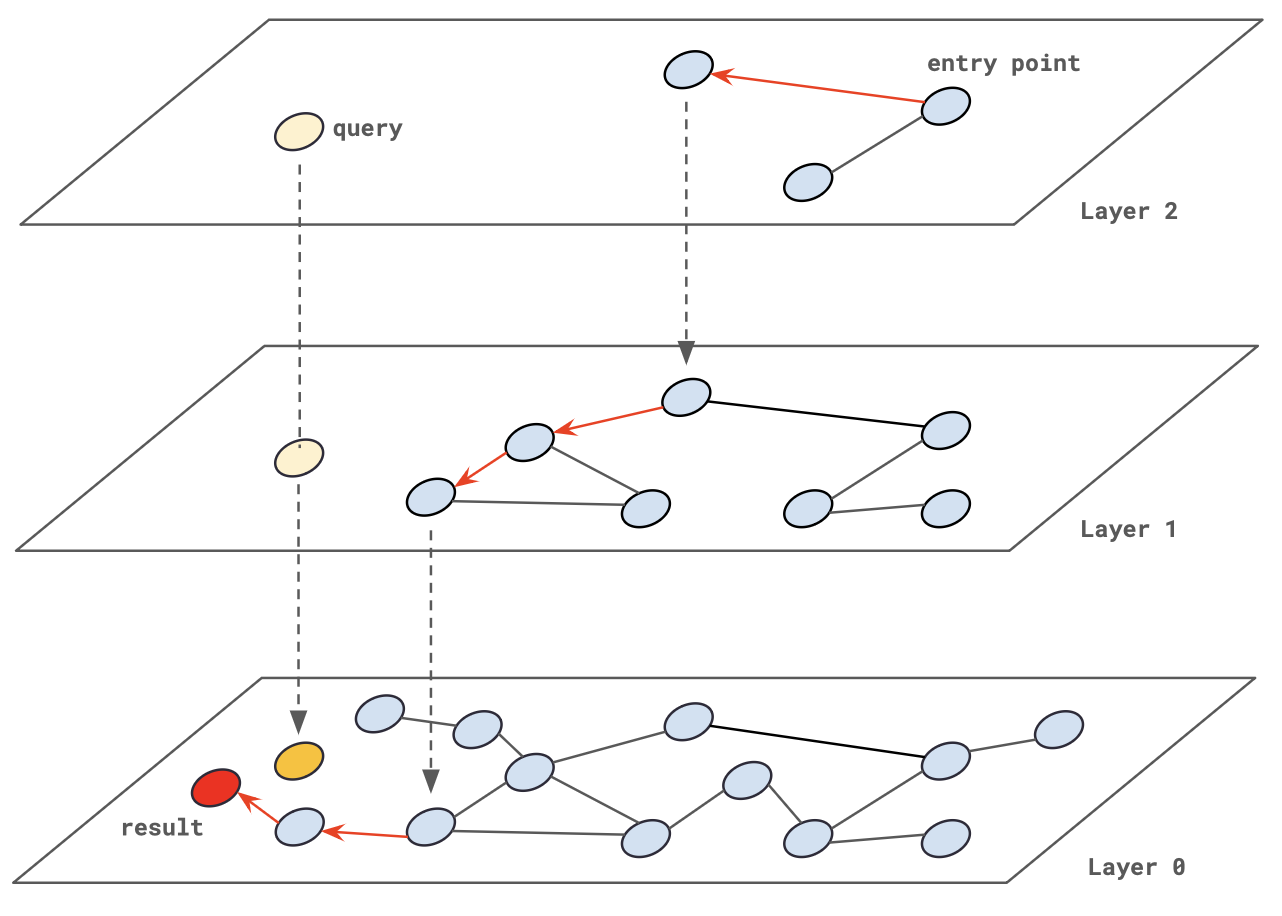
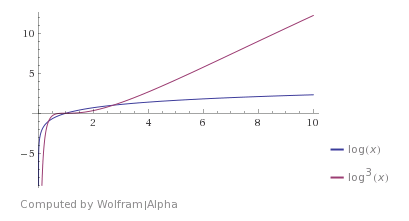
이러한 계층화를 통해, NSW가 전반적으로 polylogarithmic(붉은색 그래프)의 복잡도를 보인다면 HNSW는 logarithmic(파란색 그래프)한 수준까지 복잡도를 완화할 수 있다.
HNSW의 사용
HNSW의 벡터 인덱싱 및 검색에는 몇 가지 파라미터를 설정해주어야 하는데, 이러한 파라미터와 그 의미는 다음과 같다.
- $M$: 각 노드가 유지할 수 있는 최대 이웃의 수. 높은 $M$ 값은 검색 정확도를 향상시킬 수 있지만, 메모리 사용량과 인덱스 빌드 시간이 증가할 수 있다.
- $efConstruction$: 인덱스 생성 중에 사용되는 탐색 크기로, 생성 단계에서의 탐색 깊이와 정확도를 결정한다. 높은 $efConstruction$ 값은 더 정확한 연결을 생성하여 인덱스의 품질을 높이지만, 인덱싱 시간이 늘어날 수 있다.
- $ef$: 검색 시 사용되는 탐색 크기로, 검색 시 탐색하는 이웃의 수를 결정한다. $ef$가 높을수록 더 나은 검색 정확도를 제공하지만, 검색 시간이 늘어날 수 있다. 의미를 명확히 하기 위해 $efSearch$라 표현하기도 한다.
- $L_{max}$: 노드가 가질 수 있는 최대 레벨을 정의하며, 일반적으로 자동으로 결정되지만 사용자가 설정할 수도 있다. $L_{max}$는 그래프의 계층적 구조와 깊이에 영향을 미친다.
각 파라미터에 대한 표현은 문헌에 따라 조금씩 다를 수 있다. 파라미터의 의미를 살펴보면, 파라미터의 조정에 따라 인덱싱 및 검색의 속도와 정확도 간 trade-off가 발생함을 알 수 있다. 따라서 이 파라미터들은 데이터의 성격, 운용 환경을 고려하여 신중하게 설정할 필요가 있다.
HNSW의 사용은, HNSW 논문의 저자가 구축한 C++/Python 기반의 'hnswlib' 라이브러리를 통해 이용할 수 있다(Link). 공식 문서의 간단한 예시 코드를 살펴보면 다음과 같다.
import hnswlib
import numpy as np
import pickle
dim = 128
num_elements = 10000
# 샘플 데이터 생성
data = np.float32(np.random.random((num_elements, dim)))
ids = np.arange(num_elements)
# 인덱스 선언
p = hnswlib.Index(space = 'l2', dim = dim) # possible options are l2, cosine or ip
# 인덱스 초기화 - 'max_elements'는 반드시 사전에 설정되어야 함
p.init_index(max_elements = num_elements, ef_construction = 200, M = 16)
# 데이터 삽입
p.add_items(data, ids)
# ef를 통해 recall의 정도를 설정할 수 있다. ef 값은 항상 k보다 커야 한다.
p.set_ef(50)
# 데이터 쿼리 - k값은 반환할 이웃의 수를 설정. 결과는 두 개의 numpy array로 반환된다.
labels, distances = p.knn_query(data, k = 1)
벡터 DB에서도 HNSW 인덱스를 구성해 볼 수 있다. 오픈소스 데이터베이스인 PostgreSQL에서는 확장 기능(extension)으로 벡터 DB인 pgvector(Link)를 사용할 수 있는데, pgvector에서의 HNSW 사용 양상은 다음과 같다.
- pgvector extension 활성화
- pgvector가 이용 가능한 extension에 포함되어 있지 않다면, 먼저 github의 설명에 따라 pgvector 패키지를 적절한 PostgresSQL 경로에 다운받아 설치하여야 한다.
CREATE EXTENSION vectors;
- 벡터 테이블 생성
CREATE TABLE items (id bigserial PRIMARY KEY, embedding vector(3));
- 벡터 데이터 삽입
INSERT INTO items (embedding) VALUES (‘[1,2,3’]), (‘[4,5,6]’);
- HNSW 벡터 인덱싱
- 'embedding vector_l2_ops'는 벡터 유사도 계산 시 L2 norm(또는 유클리디언 거리)을 이용한다는 의미이다.
CREATE INDEX ON items USING hnsw (embedding vector_l2_ops) WITH (m = 16, ef_construction = 64);
- $ef$값 설정
SET hnsw.ef_search = 40;
마치며
HNSW 알고리즘은 NSW의 small world 이론을 바탕으로 한 그래프 탐색 구조에 계층화 개념을 추가하여 더 효율적인 검색을 가능하게 했다.
개념이 확장되면서 그래프 구축, 계층화, 탐색 과정의 구현이 다소 복잡할 수 있겠으나,
여러 라이브러리나 벡터 DB 제품에서 HNSW 구현이 잘 되어 있으니 크게 걱정할 필요는 없다.
다만, HNSW의 유연한 사용을 위해 벡터 인덱싱이나 검색 시 이용되는 파라미터의 의미 정도는 알아두는 것을 추천한다.
참고자료
'🟣 AI Study' 카테고리의 다른 글
| LLM이 표(table)를 잘 이해하도록 하자: Chain-of-table: Evolving tables in the reasoning chain for table understanding (2) | 2024.04.07 |
|---|---|
| ChatGPT에 질문을 해도 반응이 없을 경우 해결 방법 (0) | 2024.03.12 |
| OpenAI의 동영상 생성 모델 'Sora' Technical Report 읽어보기 (0) | 2024.02.17 |
| 검색증강생성(RAG) - 벡터 인덱스 기초 및 IVF (0) | 2024.02.12 |
| 검색증강생성(RAG) - Ragas를 이용한 RAG 파이프라인 평가 (0) | 2024.01.27 |





댓글